図1. $\omega^\omega$のイメージ図
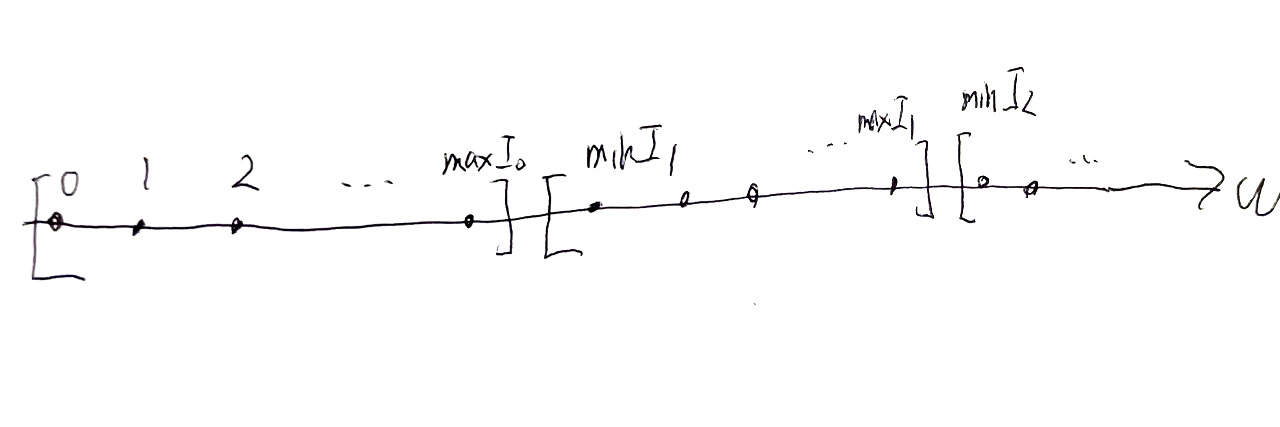
図2. $\IP$のイメージ図
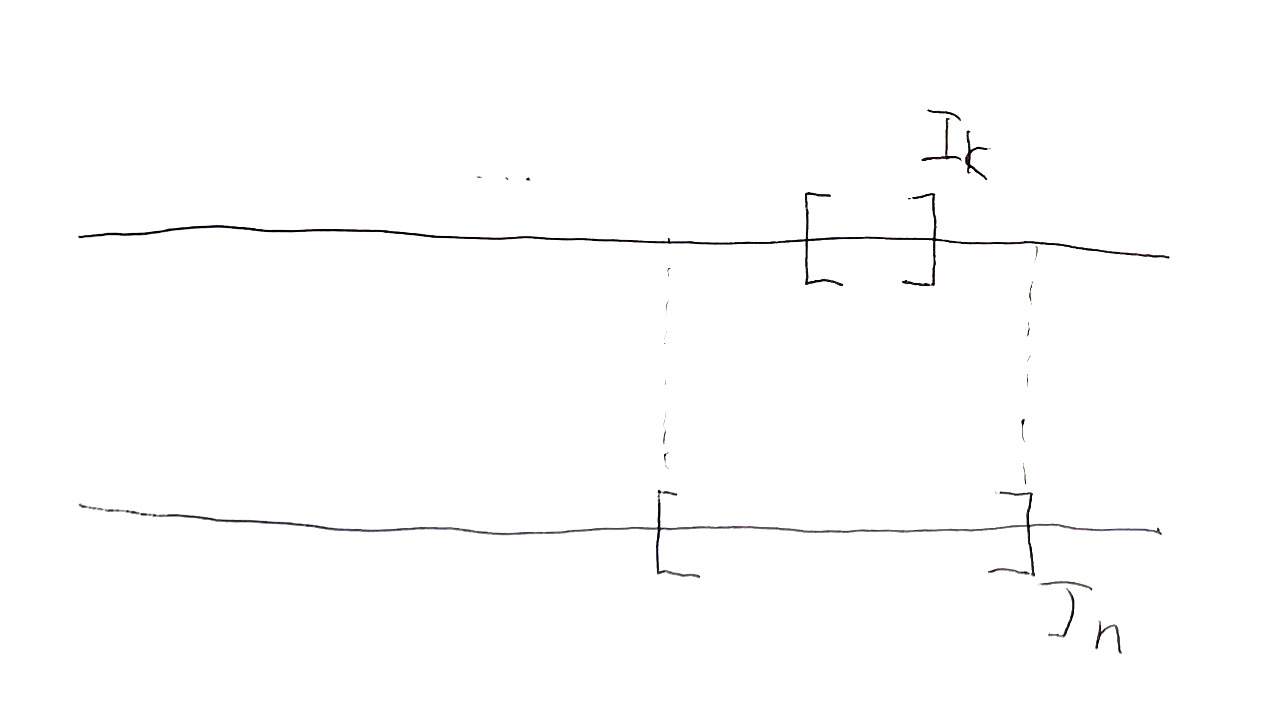
図3. $\IP$の順序のイメージ図
執筆者: 後藤 達哉, 執筆日: 2025年4月13日
この記事では自然数列のなす半順序$\omega^\omega$と区間分割の半順序集合$\IP$のTukey同値性を復習する.
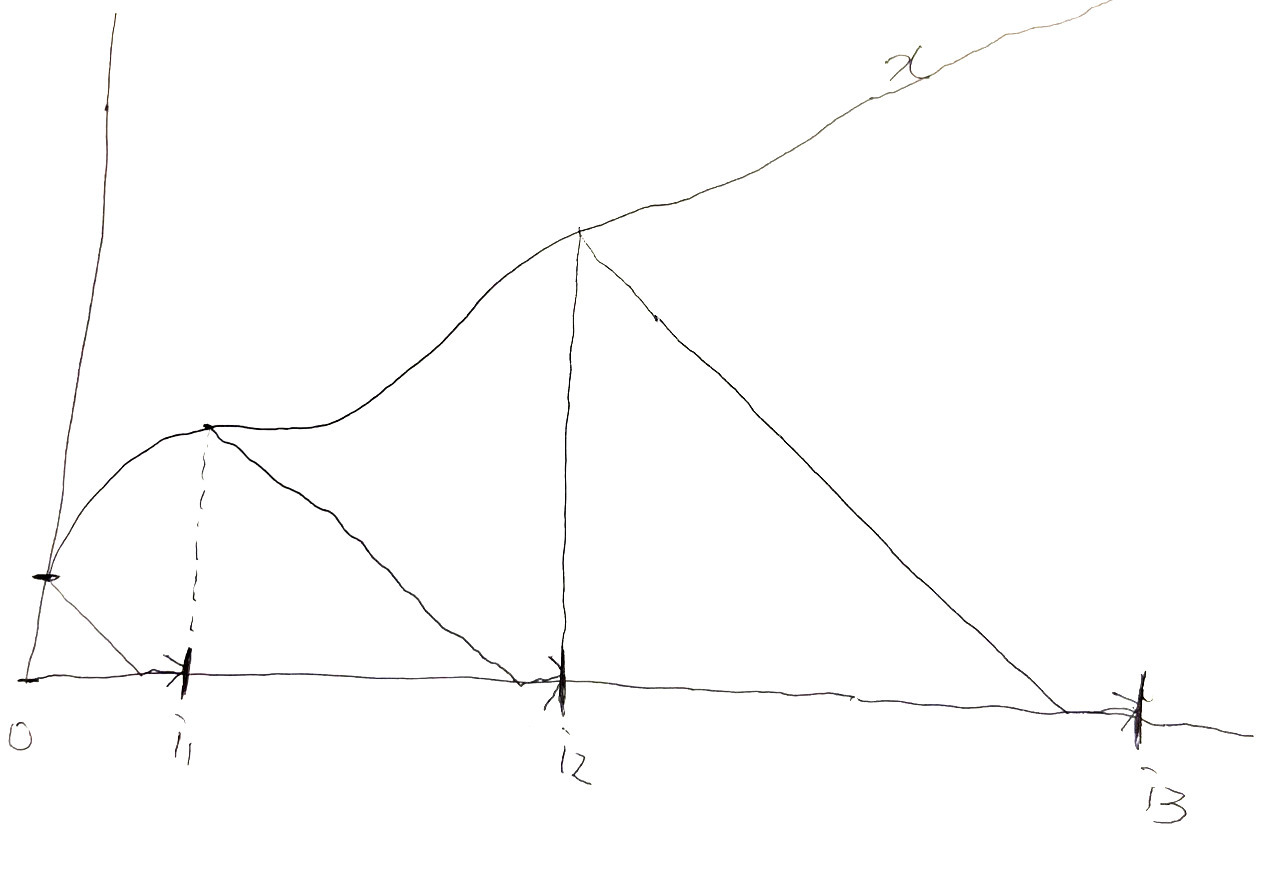
$\omega^\omega$で自然数を受け取り自然数を返す関数全部の集合を表す.すなわち自然数列全部の集合である.
$\omega^\omega$上の関係$\le^*$を次で定める: $$ x \le^* y \iff \text{有限個の$n$を除いて$x(n) \le y(n)$}. $$
$\IP$を$\omega$の区間分割全部のなす集合とする.
すなわち$I$が$\IP$の元であるとは次を満たすこと:
区間分割$I$についてはその$n$成分$I(n)$を$I_n$と下添字で書くことにする.
$\IP$上の順序$\sqsubseteq$を次で定める: $$ I \sqsubseteq J \iff \text{有限個を除いて全ての$n$で,ある$k$が存在して,$I_k \subseteq J_n$}. $$



$I \sqsubseteq J$は,$I$が$J$の細分であれば成り立つが,この順序の成立のためには必ずしもそうである必要はない.
次が本稿で復習する定理である.
次の2つの半順序集合は互いにTukey同値である.
Tukey同値という概念も復習しておこう.
半順序集合$(P, \le)$と$(Q, \le)$について$P$が$Q$よりTukey順序で下であるとは,写像$f \colon P \to Q$と$g \colon Q \to P$があって,次の条件: $$ \text{任意の$p \in P$と$q \in Q$について,$f(p) \le q$ならば$p \le g(q)$} $$ を満たすことである.
$P$が$Q$よりTukey順序で下であり,かつ,$Q$が$P$よりTukey順序で下であるとき$P$と$Q$はTukey同値であるという.
直観的には,Tukey同値性は半順序集合の共終な部分に注目したときほぼ同じ半順序構造を持っていることを表す概念である. 詳しくは,参考文献 [Bla09]の4章を参照せよ.
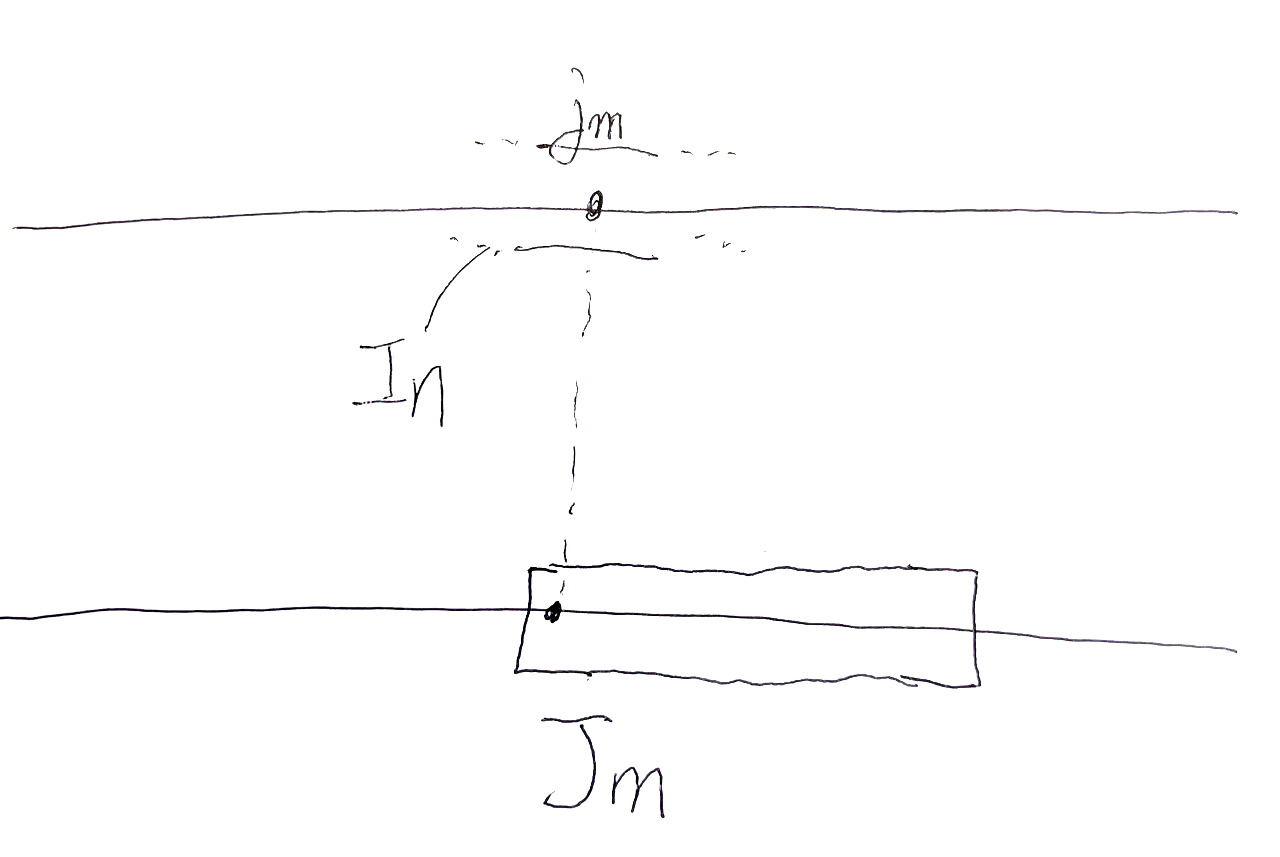
写像$\phi \colon \IP \to \omega^\omega$を次で定める: $$ \phi(I) = x \iff x(a) = \min I_{n+2} \hspace{1em}\text{(任意の$n \in \omega$と$a \in I_n$について)} $$
写像$\psi \colon \omega^\omega \to \IP$を次で定める: $$ \psi(x) = I \iff \text{任意の$n$で}i_{n+1} = \max \{ x(0), \dots, x(i_n), i_n\} + 1 \hspace{1em}\text{(ただし,$i_n = \min I_n$)} $$
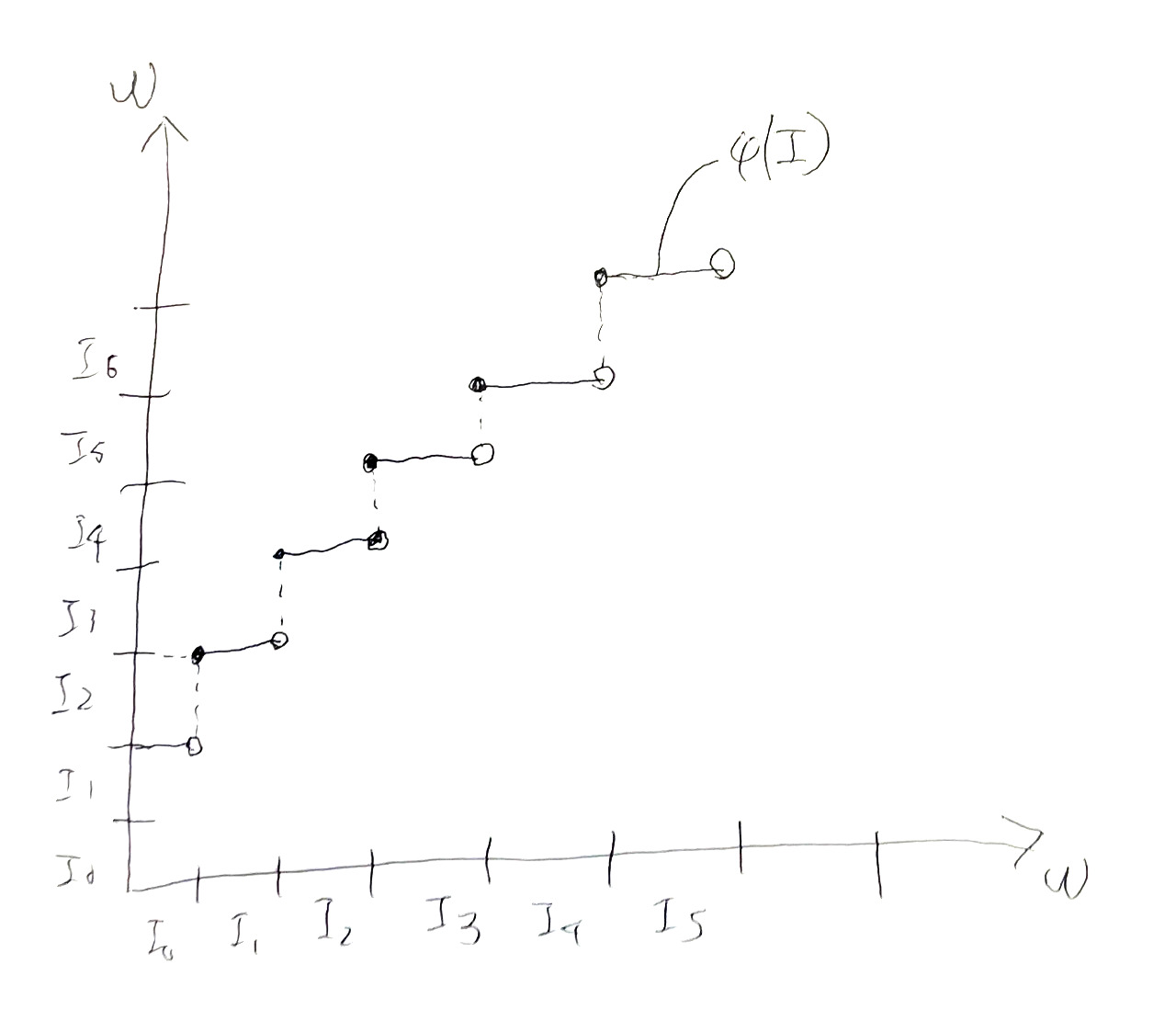
なお,$\psi$の定義は$x$が狭義単調増加関数であれば,$i_{n+1} = x(i_n) + 1$ということなので,図5のように絵に描きやすい.
こうして定められた2つの写像$\phi, \psi$について,$(\phi, \psi)$が$\IP$から$\omega^\omega$へのTukey射となっていること,$(\psi, \phi)$が$\omega^\omega$から$\IP$へのTukey射となっていることを示す.
主張の証明: $I \in \IP$,$y \in \omega^\omega$とする.$x = \phi(I), J = \psi(y)$とおく.$x \le^* y$を仮定する. すると$a^* \in \omega$を取って,任意の$a \ge a^*$について$x(a) \le y(a)$とすることができる.
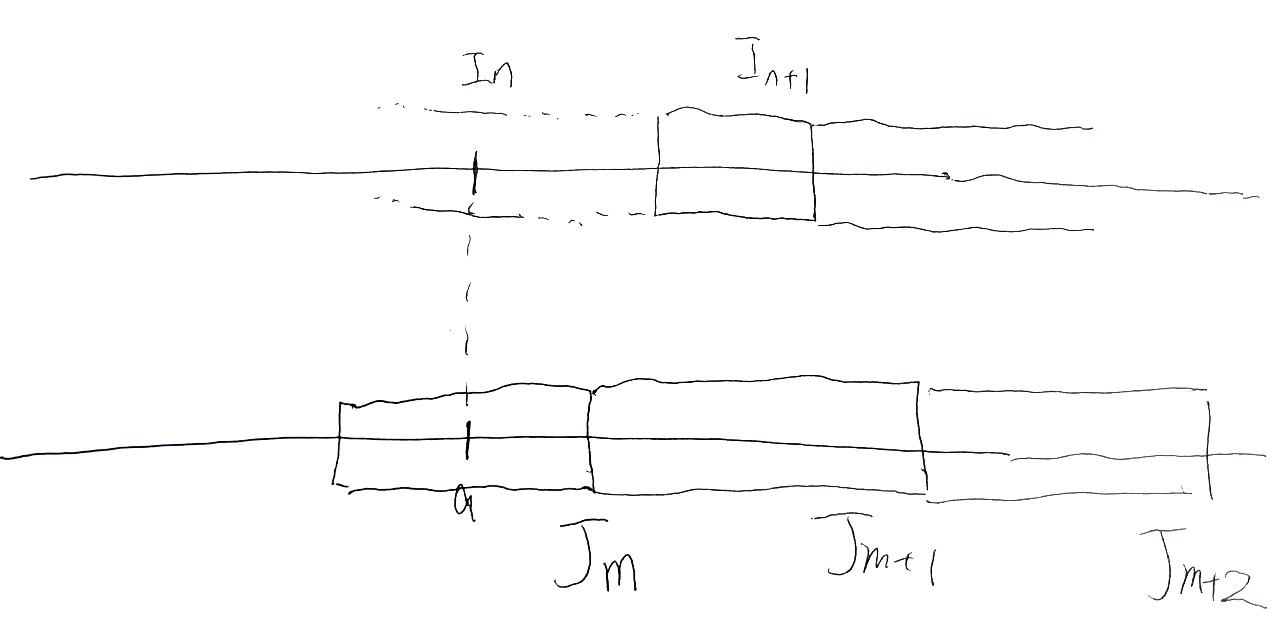
自然数$n, m$について$i_n = \min I_n$,$j_m = \min J_m$とおく.
$a^* \in I_{n^*}$となる自然数$n^*$を取る. 自然数$m^*$を$\max I_{n^*} < \min J_{m^*}$となるよう取る. $m \ge m^*$とする. このとき,自然数$n$が存在して,$I_n \subseteq J_m$となることを示せば良い.
$j_m \in I_n$となる$n$をとる.このとき$I_{n+1} \subseteq J_m$を示す. $j_m \le i_{n+1} \le i_{n+2}$は明らかであるから,あとは$i_{n+2} \le j_{m+1}$を示せばよい. しかし $$ i_{n+2} = \phi(I)(j_m) = x(j_m) \le y(j_m) < j_{m+1} $$ なのでこれは正しい. (主張の証明終わり)
主張の証明: $x \in \omega^\omega, J \in \IP$とし$\psi(x) \sqsubseteq J$とする. $I = \psi(x), y = \phi(x)$とおく. $m^*$を取って,任意の$m \ge m^*$についてある$n$があり,$I_n \subseteq J_m$とする. $a^* = \max J_{m^*}$とおく. $a \ge a^*$とする.このとき$x(a) \le y(a)$を示せば良い.
$a \in I_n \cap J_m$なる$n, m$をとる.背理法により$y(a) < x(a)$と仮定する. $x(a) \le i_{n+2}$に注意すると$j_{m+2} = y(a) < x(a) \le i_{n+2}$である. $J$の区間$J_{m+1}$に含まれている$I$の区間$I_{n'}$が見つかる. この$n'$は$n+1$でないといけない. しかし,それは$j_{m+2} < i_{n+2}$に矛盾している. (主張の証明終わり)
以上により定理が示された. (定理の証明終わり)
$\omega^\omega$と$\IP$のTukey同値性は連続体の基数不変量の不等号の証明,特に$\mathfrak{b}$や$\mathfrak{d}$が登場するものの中で役に立つ. たとえば,基数不変量$\mathfrak{b}, \mathfrak{d}, \mathfrak{s}, \mathfrak{r}$について$\mathfrak{s} \le \mathfrak{d}$かつ$\mathfrak{b} \le \mathfrak{r}$が成り立つことを示す際,$\omega^\omega$を直接使うよりも$\IP$を経由して証明すると非常に楽になる.
直観的なことを言うと、Baire空間$\omega^\omega$というノンコンパクトな空間のことをCantor空間$2^\omega$というコンパクトな空間の中で語りたいときに非常に役に立つ。